Playground Swings
(Part of joint article with Gary Williams: Swings and Slides,
Physics
Education, 40, 527 2005)
A swing may be the first playground experience. First, a
gentle swing, started by a parent. Later, demands to be
pushed higher and higher, then
slowly learning to change the moment of intertia in phase
with the motion to keep the swing going, swinging higher and
higher, experiencing the interchange between feeling heavy
and light, over and over again.
When swinging is confortable, new challenges enter: Can you
twin-swing with a friend - or can you swing faster than your friend?
How high can you swing? Is it possible to go all the way around?
How far can you jump - and when is the best time to jump?
A swing is an example of a pendulum, familiar to everyone.
It provides an abundance of physics examples, and children's
questions often enter territories
well beyound the curriculum. The experience of the body
can be enhanced by visual measurements using simple
equipment, that may make more difficult concepts available.
Returning to these questions
in school helps enforce the
notion that physics is not only about equipment in the
classroom, but concerns everything around us.
Force and acceleration
In a mathematical pendulum, forces act on an inanimate,
pointlike object. In a swing, the forces act instead on
the body that is your own. Close your eyes and recall the
feeling. In which direction does the force from the swing
act on you? When is this force largest (smallest)? How large (small) does it
get?
The chains holding the swing can exert a force only
along the direction of the chain. The force from the swing
on the rider will thus always be directed to the suspension
point. The length of the chain is constant. As the swing turns
at the highest points, the force from the chain counteracts the
radial component of the force of gravity. The larger the angle of
the swing, the smaller the force of the chain at the turning point.
The orthogonal component of mg gives rise to an angular
acceleration, bringing the swing back down again.

|
Figure a: A spiral rabbit has an internal spring scale
measuring the force acting between the feet and the head. The figure shows
the appearence of the rabbit for
weightlessness (0g), normal load (1g) and for a motion giving
approximately 2g (as, e.g., in an upward acceleration of 1g). The resolution can be
increased by holding the rabbit upside down, since the head is heavier.
|



Figure b: A slinky and a spiral rabbit.
Note that they are both short at the turning points, and considerably
expanded at the bottom (although the rabbit's ears prevent maximum
expansion). Air resistance slows the motion of the outer
parts of the slinky.
|
Measuring the experience of the body
The feeling in your stomach tells you that for an accelerated body,
forces do not act only in the contact area, but propagate throughout
the body, so that a sufficient net force, F=ma, will be
exerted on every ounze to provide the required acceleration. The body
thus experiences acceleration much in the same way as gravity.
The concept "g-force" is useful to describe this experience.
Children have heard about the concept, but it is rarely introduced
in textbooks, let alone defined. Let us
introduce a "normalized force"
f=(a-g)/g,
which is the force, in addition to gravity,
acting on an object, divided by the weight,
mg, of the object.
For a free fall, this normalized force becomes zero. For an object
at rest, the vector f has unit magnitude, and is directed
upwards, i.e. in the direction of the force required to counteract
the force of gravity.
As the swing turns at an angle 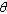 ,
the magnitude of f is g cos
,
the magnitude of f is g cos
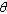 ,
directed along the chain, towards the point of suspension.
As the swing passes the lowest point, the chain must counteract mg,
but also provide the centripetal force, m
v2/r. For a mathematical
pendulum, the acceleration at the lowest point is 2g(1-cos
,
directed along the chain, towards the point of suspension.
As the swing passes the lowest point, the chain must counteract mg,
but also provide the centripetal force, m
v2/r. For a mathematical
pendulum, the acceleration at the lowest point is 2g(1-cos
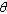 ),
independent of the length of the pendulum. The "g-force" then
becomes 3-2 cos
),
independent of the length of the pendulum. The "g-force" then
becomes 3-2 cos
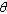 .
.
The experience of the body can be illustrated by bringing along a
small slinky or a spiral toy, as shown in Figures a and b, which
gives a real-time visual measurement of the varying forces during a swing.
The spirals are shortest at the turning points and most expanded at
the bottom.
Student expectations are unlikely to coincide with these
observations. Often, the
acceleration is subconsciously used in the everyday sense of "increase of
speed", or possibly "change of speed". Obviously, the rate of speed change is
largest at the turning points and zero at the bottom, where speed has a maximum.
The insight that acceleration in physics is the time derivative of velocity,
which is a vector, does not come easily to most students, who are likely to
have been brought up on an "acceleration diet" consisting of one-dimensional
motion, often starting from rest. Still, the more general concept of
acceleration is evident throughout the body, and clearly visible in the simple
measurements - or in the accelerometer data described below.

Figure c: Electronic measurement of the g-force in a playground
swing. The accelerometer was held with the arrow pointing in the direction of
the chain, for nearly 30 seconds.
It was then turned to lie along the direction
of the motion, measuring the tangential component of the g-force.
|
Electronic measurements
Figure c shows a graph from an electronic measurement of g-forces in a
playground swing. The probe is a Vernier 1-D accelerometer /1/, held with the
arrow in the direction of the chain. The period in the graph is only half the pendulum period, since the
swing passes the lowest point twice during a period.
The smallest values correspond to
cos 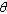 , where
, where
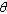 is
the angle at turning. Similarly, the largest values correspond to gravity plus
the centripetal acceleration, giving (3-2 cos
is
the angle at turning. Similarly, the largest values correspond to gravity plus
the centripetal acceleration, giving (3-2 cos 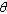 )
for a point-like
pendulum. (Note that the deviation from unity is twice as large for
the maximum g-forces compared to the minimum.)
)
for a point-like
pendulum. (Note that the deviation from unity is twice as large for
the maximum g-forces compared to the minimum.)
During the last part of the graph the accelerometer probe was held with the
arrow in the direction of motion, resulting in very small values, as discussed
below.

| Figure d: Bringing along a bottle with a small amount of coloured
liquid provides a challenging demonstration of forces in a pendulum motion.
|
Tangential components of the acceleration
The speed changes in the swing results from the component of the
gravitational force along the motion. Still, measuring this
component gives very small values, which is quite
counter-intuitive. However, since gravity is the only
force in the direction of motion, that component of
acceleration will be exactly the tangential component of
g, resulting in a zero component of a-g
as seen in the
graph. A one-dimensional accelerometer is thus sufficient to measure the
forces on the rider in a swing - but it is important to understand that it is
not
measuring acceleration, but a component of the g-force. A
three-dimensional
accelerometer would provide no additional information in this case.
The vanishing tangential component of the g-force for the rider in a
swing
can also be illustrated by bringing along a bottle with a small amount
of
coloured liquid at the bottom (Figure d). Students who tried it have
asked for
water to
dilute the liquid, so it would flow more easily during the motion - only
to
discover that the surface of the liquid does, indeed, remain parallel to
the
swing. The water level is orthogonal to the plumb line, in this case
represented
by the chain.
A similar experiment can be performed in an amusement park pendulum
ride,
bringing along either a small (soft) mug of water (1 cm is sufficient),
or a
small cuddly animal on a short string. (Safety must always come first!)
What do you think will happen?
Will the result depend on whether you sit in the middle or in the back?
Will you come off the ride complaining that there must be something
wrong with your water, since it didn't move?

| Figure e: Accelerometer data for a 42 m
long swing.
|
The period of a swing
The period of a pendulum is remarkably independent of the angle, as
noted
already by Galileo. This "iso-chronism" forms the basis of a pendulum
clock,
and it is easy to remember that the second-pendulum (where the
half-period is 1
second) is about one metre, giving us an easy way to estimate the period
for
pendulums of varying length, using the relation for a mathematical
pendulum,
T=2 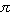 (g/L)1/2.
The independence of the period on the mass of the pendulum is, of
course, a
consequence of the equivalence principle. Children can "twin-swing"
reasonably
well, with an empty swing, or with another child essentially independent
of size.
(g/L)1/2.
The independence of the period on the mass of the pendulum is, of
course, a
consequence of the equivalence principle. Children can "twin-swing"
reasonably
well, with an empty swing, or with another child essentially independent
of size.
Real-life pendulums often have slightly longer periods, than given
by the formula, above.
Although large angles leads to longer periods, this rarely accounts for
the
deviations found by the students, who are also more likely to blame
deviations
on energy losses. That neither effect has a large influence on the
period can be
seen in the accelerometer graph (Figure e) from a 42 m long swing
hanging
from a suspension bridge in the harbour of Göteborg during April 2002
/2/.
The length of this swing provides a curious mixture of speed, in the
passing of
the lowest point, and a very slow pendulum due to the long chains.
Swings of similar length can also be found in several amusement
parks. The effect of air resistance,
proportional to
v2 can no longer be neglected for the high speeds in
these long swings, resulting in the strong damping, evident from
the accelerometer graph, as well as from observation of the swing.
A more important factor affecting the period is the moment of inertia.
Although students are not necessarily familiar with this concept, they
understand that
an object hanging from the center of mass will not swing, or that a
counterweight, such as in the ride in Figure f, will result in a longer
period.

|
Figure f: An amusement ride /3/ where riders sit about 13m from
the
center, but with a half-period of about 10 s (for small angles). The
long period
is due primarily to to the counterweight, partially hidden behind the
tree.
Since this pendulum is stiff, rather than suspended in a chain, it is
possible to complete a 360o turn, nearly stopping at the top.
|
Using swings in physics teaching
The physics teacher returning to the playground as a parent,
pushing children, may reflect on the equivalence principle that allows
children to twin swing independent of mass,
on the forces acting on children, on
angular momentum or energy conservation. The experiments in jumping off
the
swing at various parts of the ride may be replaced by numerical
simulations to
find the best angle. A collaboration with the PE teacher can invite
projects investigating e.g. the physics of trapeze /4/.
Swings come in many varieties, and their physics offer insights in many
fundamental principles. Emphasizing the forces acting on the human,
accelerated
body, shifts the focus from centrifugal to centripetal forces, which may
be useful for "cracking the code" that F=ma.
References
- Vernier, Low-g accelerometer,
http://www.vernier.com
- Monica Sand, Can gravitation be cancelled
http://www.zerogravity-art.nu/
- The Looping Starship by Intamin,
http://www.intaminworldwide.com/
- The physics of Trapeze,
http://baltimore.trapezeschool.com/resources/physicsintro.php




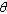 ,
the magnitude of f is g cos
,
the magnitude of f is g cos



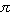 (g/L)1/2.
The independence of the period on the mass of the pendulum is, of
course, a
consequence of the equivalence principle. Children can "twin-swing"
reasonably
well, with an empty swing, or with another child essentially independent
of size.
(g/L)1/2.
The independence of the period on the mass of the pendulum is, of
course, a
consequence of the equivalence principle. Children can "twin-swing"
reasonably
well, with an empty swing, or with another child essentially independent
of size.
