Himmelskibet - Star Flyer

Number of Swings: 12 (each with 2 seats) Elevation: 80 m Star diameter: 14 m Chain length: 8 m Turns/minute: 10 Vertical speed: 2.2m/s

Opened 12 April 2006 Capacity: 480/hour Himmelskibet www page Funtime Patent: WO2004067126 Technical drawing

1. Observe the ride as it starts moving. What factors determine the angle of the swings?

2. How do you expect the angle to depend on the number of people (0, 1 or 2) in a pair of swings?

3. The forces acting on the rider are the force, mg, of gravity and the force, T, from the swing acting along the line of the chain. Use this information to draw a free-body diagram.

4. What is the the acceleration of the rider during different parts of the ride?

5. Take a look at a Movie of Himmelskibet in action. Use the movie to estimate the time for a full circle

6. The graphs below show accelerometer and elevation data for the whole Himmelskibet to The top graph shows the ratio | (a-g) / g |. Use the graphs to estimate the horizontal acceleration during the main part of the tour.

7. How fast must the swings move to experience this acceleration for the rotation time above?

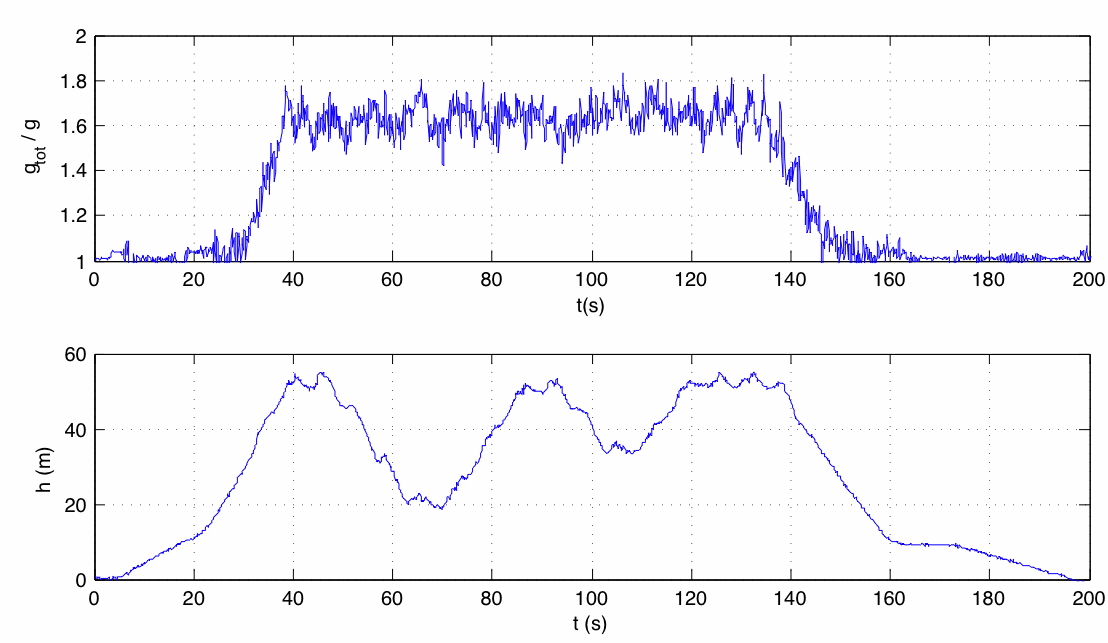
See also the graphs over the relations between the angle, and rotation period, acceleration and speed.

Gravity and acceleration - for planets and rides

That the angle is the same for swings with 0, 1 and 2 riders is a small-scale version of a classical experiment by Eötvös. It illustrates the "equivalence principle"- that the "gravitational mass" (in m g) is the same as the "inertial mass" (in m a). In the case of the swings in Himmelskibet, the angle is given by arctan (m|a|/m|g|) = arctan (|a/g|), which is independent of mass.

The equivalence principle was also illustrated by the early physics giant, Galileo Galilei, in the famous experiment of comparing the time of falling for cannon balls of different size. Much later, the equivalence principle inspired Albert Einstein to consider the general theory of relativity. Read more.