Many modern roller coasters features loops. Although textbook loops are often circular, real roller coaster loops are not. In this paper, we look into the mathematical description of various possible loop shapes, as well as their riding properties. We also discuss how a study of loop shapes can be used in physics education.Keywords: Acceleration, force, roller coaster, loop, clothoid
Figure 1: Examples of loop shapes. The red loop to the left is from Loopen at Tusenfryd in Norway (Vekoma, Corkscrew, 1988) . The yellow loop in the middle is from HangOver (Vekoma, Invertigo, 1996) at Liseberg, now relocated to Sommerland Syd in Southern Denmark. The loop to the right is from the newly opened "Kanonen" (Launch Coaster, Intamin/Stengel, 2005) at Liseberg [1]. Exercise for the reader: The Kanonen train has a length of 9.5m and takes about 1.3s to pass the top of the loop. Use the photograph to estimate the g-force of the rider in the top of the loop. Does it make any difference whether you sit in the front, back or middle? How much?
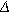h.
At any given part of the frictionless roller coaster,
the centripetal acceleration is thus given by
ac= v2/r = 2gh/r
where h is the distance from the highest point of the roller
coasters and r is the local radius of curvature.
Assume that you pass the top of a loop with a speed v0, obtained e.g. by starting from rest at an height h0=v02/2g above the top of the circular loop. If the loop has a radius, r, the centripetal acceleration at the top will be a0=2g h0/r. The centripetal accelerations at the side and at the bottom are immediately obtained from the value at the top as (a0 + 2g) and (a0 +4g), respectively.
The limiting case of weightlessness (0g) at the top, where no force is needed between train and track, nor between riders and train, occurs when h0=r/2, so that the centripetal acceleration is given by a0=g (and the centripetal force is thus provided exactly by the gravitational force from the earth). The centripetal acceleration at the sides and bottom will be 3g and 5g, respectively. (What is the total acceleration of the rider for these cases?) The corresponding "g-forces" are 3g and 6g.
Trains moving slowly across the top would fall of the track, were it not for the extra sets of wheels on the other side of the track. Similarly, the riders would depend on the restraints to remain in the train. However, even if the train were nearly at rest at the top, with riders hanging upside down, experiencing -1g, the riders would still be exposed to 5g at the bottom (and 2g at the side) if the loop were circular.
Children's roller coasters may be limited to 2g, family rides often reach 3g, sometimes more, whereas many of today's large roller coasters exceed 4g. Depending on the individual's "g-tolerance", the oxygen supply to the head may stop completely at 5 to 6 g, resulting in unconsciousnes if extended in time. Although higher g-forces can be sustained with special anti-g-suits, e.g. for pilots, 6g for any extended period of time would not be acceptable for the general public [2].
However, the disadvantages of circular loops are not limited to the maximum g-force at the bottom: Entering the circular loop from a horizontal track would imply an instant onset of the maximum g-force (as would a direct transition a circular path with smaller radius of curvature). An immediate transition from one radius of curvature to another would give a continuous, smooth track, but with discontinuous second derivatives. Clearly, a function with continuous higher derivatives would be preferrable. From the loop photos in Figure 1, it is obvious that different approaches have been used to achieve the desired transition from a smaller radius of curvature at the top to a larger radius at the bottom. Below, we discuss a number of possible loop shapes with this property.
This set of coupled differential equations can be used in a spreadsheet program or used in an ordinary differential equation (ODE) solver e.g. in matlab. The difference between the different loop types is reflected in the expression for the curvature, (i.e. 1/r), as discussed below.
Thus, the radius of curvature varies linearly with elevation. This condition could be applied for the whole loop or only for the lower part of the loop, which is then matched with circular track for the upper part, as illustrated in Figure 2 for the cases of ac=2g and 3g, respectively. Figure 3 illustrates the influence of the matching angle on the loop shape for a constant centripetal acceleration ac=3g.
For this type of loop, the force from the track on the train
increases continuously, as the component normal to the track
of the gravitational acceleration,
g cos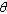 
,
increases. The maximum g-force
for the rider will thus be ac + g = (ac/g + 1)g.
The condition of constant centripetal acceleration results in a loop shape that is symmetric around the lowest point, and the loop shape could be extended into repeated to generate a sequence of loops. An example of a double loop can be found in the Great American Scream Machine from 1989 [1]
Figure 2. Different loop shapes for the condition of constant centripetal acceleration. The first two loop shapes give a centripetal acceleration of 2g and 3g, respectively, throughout the loop, (for a particular velocity), whereas the last two loops maintain these conditions only for the bottom part of the loop, matched to a 120o circular arc at the top. The loop with 3g centripetal acceleration throughout the loop is very similar to the Invertigo loop in Fig. 1.
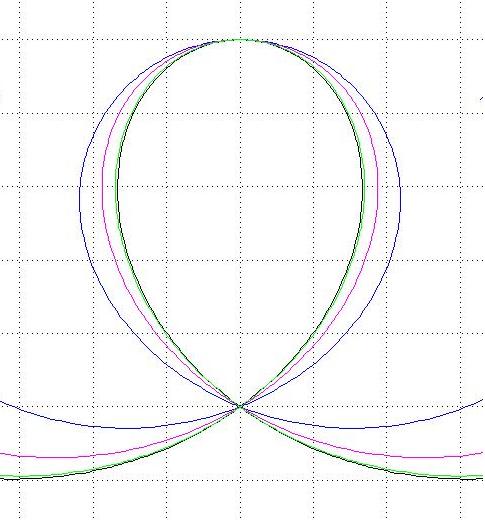
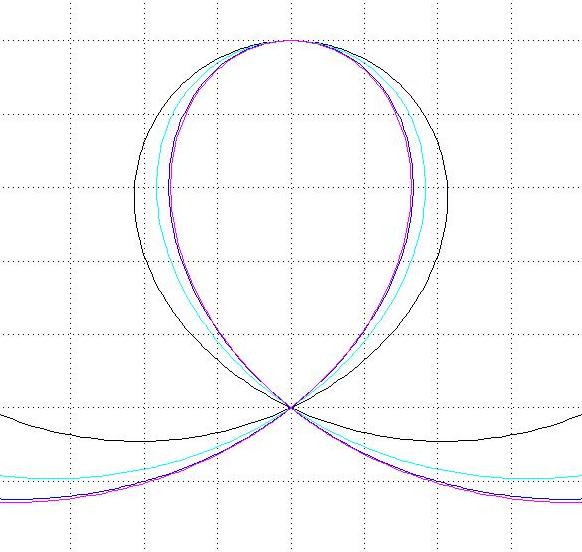
| Figure 3 Loops generated using the condition of a constant centripetal acceleration ac=3g matched to a circular arc covering the top 0o, 60o, 120o and 180o, respectively. The loops are normalised to give the same distance between the highest point and the "intersection". The widest loop is then obtained for the matching where the track is vertical and the narrowest when the condition is applied throughout the loop. | Figure 4 Loops generated using the condition of a constant g-force of 4g matched to a circular arc covering the top 0o, 60o, 120o and 180o, respectively. The loops are normalised to give the same distance between the highest point and the "intersection". Just as in the case of constant centripetal acceleration, the narrowest loop is obtained when the condition is applied throughout the loop. The grid has been kept in the diagram to facilitate comparison with the similar, but slightly wider loops shown in Figure 3. |
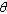0
with the horizontal, has a local radius
of curvature r0, and the centripetal acceleration is, again,
given by ac,0=2gh0/r0.
The g-force factor is given by the force from the train on the rider divided by the weight of the rider, which can be expressed as a vector f = m(a-g)/mg = (a-g)/g. In the matching point to the circular arc the vector a-g has the magnitude
In order for the g force to remain constant, the radius of curvature must depend on the height and slope of the track as
This is then the condition to be inserted in the specification of the ordinary differential equation determining the curve. As in the case of constant centripetal acceleration, the curve is symmetric around the lowest point and the condition of constant g-force can be maintained throughout a sequence of loops - although the riding experience may not be that interesting.
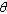/ds=as,
some algebra is needed to express the boundary conditions in a
convenient form, since the parameter, s, is not easily available in
relation to the position in the loop.
Integration of the angle gives
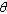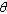=0 + a s2.
If the Cornu spiral is oriented with the center sloping downwards
the track will pass a lowest point between the loop and the
center of the clothoid. At this point the radius of curvature will be
larger than at the top or the side of the loop. The ratios between
these radii of curvature may be one
way to specify the clothoid.
Figure 5 shows examples of s clothoid loops where
the center of the Cornu spiral is horizontal.
The Looping Star was an early implementation of this
shape, which also gives a good fit for the Kanonen loop.
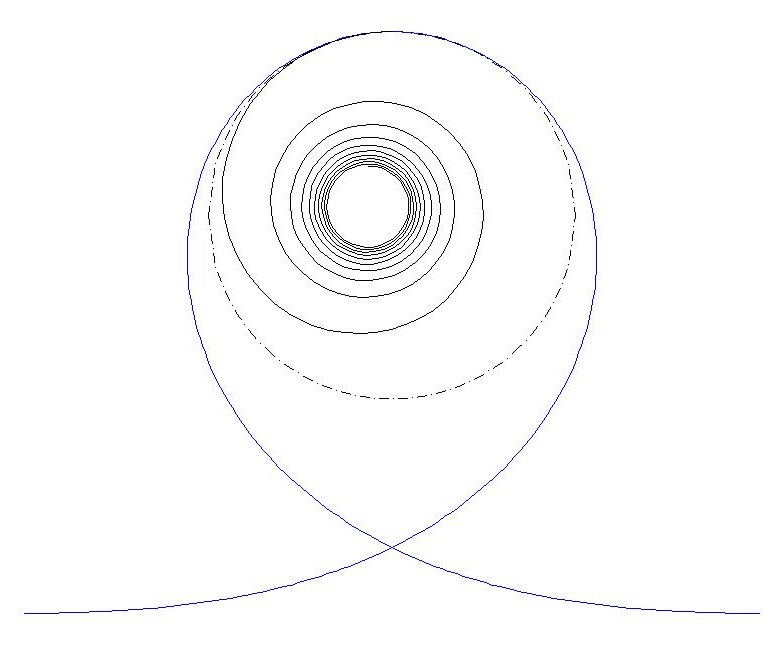
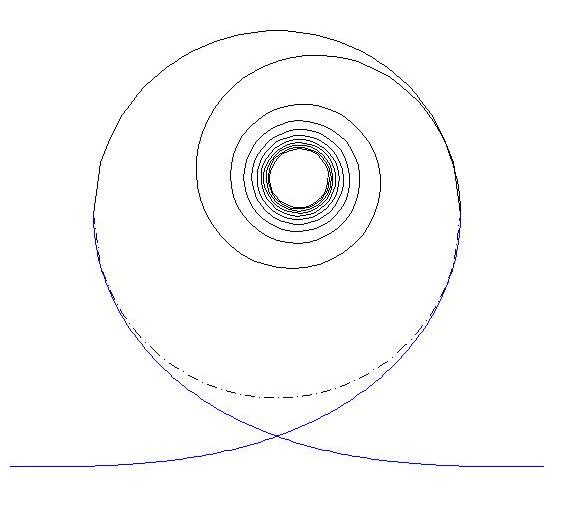
Figure 5 Examples of clothoid loops, where the track enters horizontally. In the loop to the left, clothoid extends throughout the loop, whereas in the loop to the left, the top is a half circle, matched to the cornu spiral where the track is vertical. For these choices, the angle at the intersection is about 127o and 141o, respectively. The continuation of the spiral is shown as an illustration, together with the circle corresponding to the radius of curvature at the top.
Can we find the critical parameters that specify a loop? The width at the widest point in the loop can provide a suitable length scale. The height difference between this "waist line" of the loop and the highest point indicates if the upper part is a half-circle or whether an alternative loop shape is used also for this part. (A problem, however, is that it is often hard to find a photo angle that gives you a clean profile.) Other characteristic properties are the angle where the tracks "intersect", the elevation of the top (and of the lowest point, if there is one) relative to the intersection. All these depend on the loop type and on the parameters chosen for each type.
Another key would be the riding properties. Accelerometer data [6] for Invertigo [2], e.g., show that, the g-force at the bottom just before and after the loop are about 4.5g and 4.0g, respectively, and about 2.2g at the top, consistent with an essentially constant centripetal acceleration of about 3.2g [7]. Comparison with the data for the reverse tour, shows that the difference between the g-factors before and after the loop are not due to the shape of the track but to energy losses, which happen throughout the ride. The loop shapes discussed in this paper reflect physics as the "Art of systematic oversimplification". The accelerometer data from the Invertigo ride immediately show that friction cannot be neglected.
To make a program to draw loops of various types, generate the corresponding loop and loop measures, and compare to a few real loops would make for a challenging student project. A test of the fit can be obtained by printing a photo of the loop onto a transparency and then change the size of the calculated graph on the computer screen (or resize directly in a layer in a drawing program). Smaller computational projects can be to provide students with coordinates for a particular loop shape. If desired, coordinate may be revised to distinguish between "heartline" and the track, both for the case of an ordinary and a suspended ("inverted") coaster. Students can then be asked to work out e.g. radius of curvature as a function of elevation or angle, the time required to complete the loop and the time variation of the g-forces on the body [8]. For increased difficulty, energy losses may be taken into account.
A special aspect is the effect of the length of the train. In fact, the choice of loop shape is often related to the train length, as reflected in the loops in Figure 1. (See also other loops in the RCDB [1]). For a longer train, the center of mass lies further below the top, making a higher and narrower loop desirable [9]. Calculating loop shapes may permanently change the way you view a roller coaster loop.
