| Figure 1: A pendulum experiment with a cuddly toy on a string in a playground carousel. |
A carousel gives possibilities to explore physics in rotating systems and to gain first-hand experience of methods to measure rotation, without the need for an external reference. This paper discusses the Foucault pendulum, a well as the sideways deflection of horizontally and vertically moving objects in a rotating system. These experiments lay a foundation for an understanding of ways to demonstrate that the earth spins around its axis.PACS: 01.40.-d, 01.40 Fk, 01.40.Ej
But how do we know? Anyone who has observed Foucault's classical pendulum in Pantheon in Paris, or a science center or science museum version, is unlikely to forget it's slow, very slow, change of the direction of swinging relative to the floor. Most of our new students have not seen it. We could shift the question of the spinning earth to focus on how we can know if anything rotates. The need for a centripetal force to keep the body in a circular motions is felt in the body of anyone in a swing or in a fast-moving carousel, although the experience is often discussed in terms of a centrifugal force. In a slow carousel or rotating tower, this effect is not very conspicuous. On the other hand, the much less familiar Coriolis effect for bodies moving in rotating systems can be observed in simple and small-scale experiments, that are still quite spectacular. The experiments can be peformed in an amusement park or in a local playground carousel, where the playground has the advantage of easier access. It can be visited more frequently and experiments can be repeated if additional questions arise during follow-up discussions after the visit. In addition, safety considerations are less stringent in a playground, which makes it possible to bring more objects into the rotating systems.
Recently, I invited a class of fourth-graders (10-11 year olds) to experiment at a large playground in Göteborg. Experiments were performed carousels, as well as in swings and slides (Pendrill and Williams, 2005) and in a climbing rack. At the end of the visit, the whole class sat down and discussed the experience before returning to school, and I asked what experiments had surprised them most. They agreed that the experiments in the carousel had made the strongest impression. This paper discusses these experiments.
| Figure 1: A pendulum experiment with a cuddly toy on a string in a playground carousel. |
Adults without physics training often have difficulties with the pendulum experiment. Instead of letting the object swing, they typically let it hang still and wait for it to move outwards when the carousel starts. Adults know what happens when things go around. However, of the inertial forces appearing in a rotating system the centrifugal force is not very eye-catching in a slow carousel, whereas the Coriolis effect for moving objects makes the pendulum experiment rewarding for those who follow the instructions. I have observed 8-year olds coming off an amusement park carousel and excitedly tell their friends and teachers that "It made a star, it made a star." Another 8-year old described how the pendulum in a panorama tower kept moving towards a tall building in the harbour. Asked to explain the motion he said that it would not have moved like that if it had instead been the windows and everything outside moving around the tower.
The pupils in the playground were absorbed by watching the little pendulum swing, as in Figure 1. Earlier work (Bagge and Pendrill, 2002), presented the results of interviews with another group of 10-year old three months after an amusement park visit which included carousel experiments. The visit had taken place just before Christmas, and the class teacher was concerned that he had not had time to follow up on their experiences in the park. During the group interviews, many of the children recalled the pendulum in the carousel, and also that it had something to do with the rotation of the earth, commenting e.g.:
"In the Pony Carousel, the cuddly toys on the strings started to move like this. I think it was to prove that the Earth is rotating."This quote was accompanied by drawing a star in the air. During the visit, one of the teachers in the class had brought up the question why we would do this, so the question how we can know that the Earth rotates was discussed. For some children, this discussion had made a deep impression.
"I learned that when going in the Pony Carousel, the cuddly toy kept going in the same direction while I was going around."
Here, the response indicates an awareness of two different system, one rotating and one non-rotating.
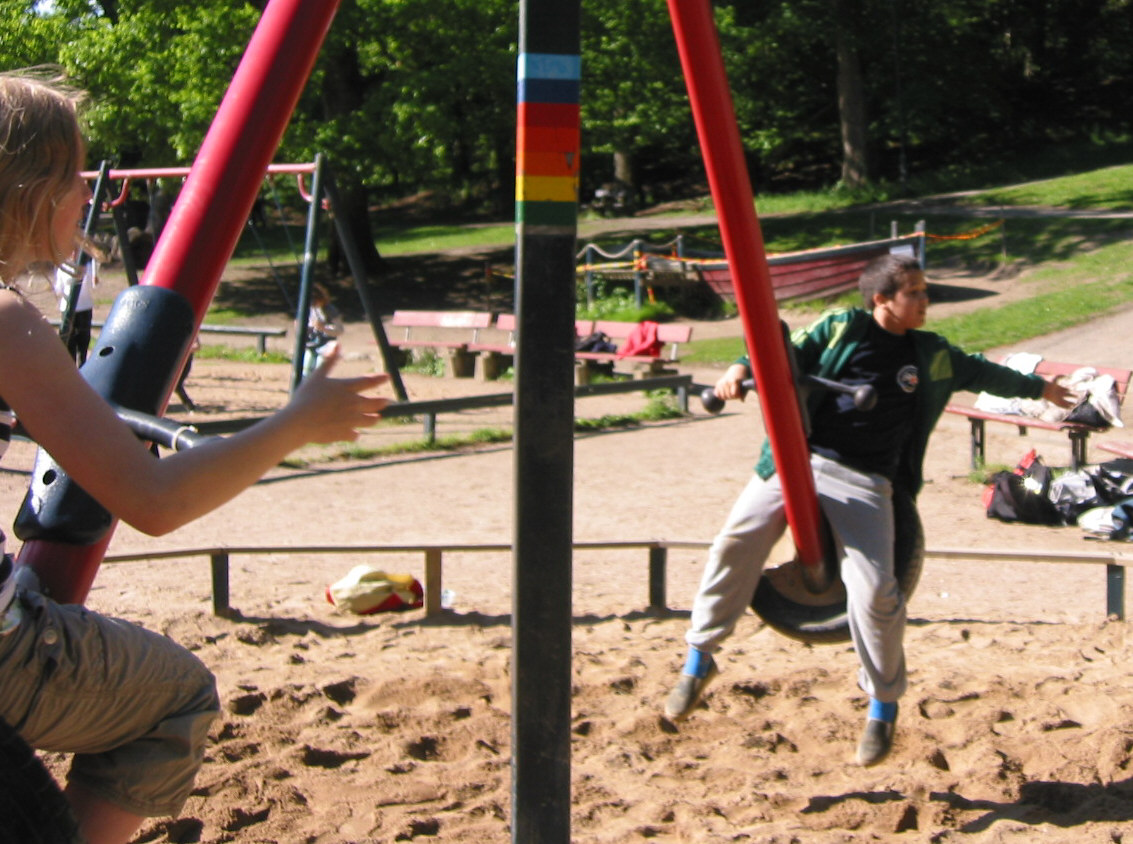
| Figure 2: Two fourth graders throwing ball in a playground carousel which rotates counter-clock-wise. In the first attempts, the ball arrives behind the person on the other side. |
In the discussion after the experiments, they children could describe how they had figured out that they needed to throw the ball a little bit to the front of the friend on the other side, since he would have moved a bit before the ball arrived. (The fact that the ball has an initial sideways velocity due to the rotation was not brought up.)
On special occasions, experiments requiring additional preparation might be performed in an amusement park. Mühlen et al. (1999) describe experiments in the Gröna Lund amusement park, where a water pistol was mounted in a preconstructed rack, so that the water was shot towards the center of the carousel. In another experiment an airgun and a shooting target was mounted under a carousel horse, and the difference in arrival points for a stationary and rotating carousel could be clearly discerned.
|
|---|
| Figure 3: An experiment to measure the deviation of a falling marble when the carousel is in motion. |
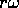, if
viewed by an imagined stationary overhead observer. This motion will
bring the marble slightly further from the center of the carousel, where
it's speed will be insufficient to keep the same angular velocity as the
carousel. The landing point for the marble will thus be slightly outside
and behind the pole.
An analysis of the motion of the marble using inertial forces must include both the "centrifugal" and "Coriolis" force. Since the Coriolis force is proportional to the velocity component orthogonal to the axis of rotation in the moving system, the downward motion, being parallel to the axis, does not contribute. The initial outwards deflection is a consequence of the centrifugal force. The resulting outward motion, as seen from within the moving system, can then lead to a contribution to the Coriolis force, giving rise to the apparent backwards deflection.
The experiment with marbles falling in a carousel can be seen a simplified miniature version of an experiment suggested in the 17th century as a way to prove or disprove rotation of the Earth, as discussed in detail by Persson (2003, 2005). During the winter 1678-1679, Newton and Hooke debated the trajectories of falling objects. Thanks to Hooke, Newton came to the insight that the falling body would follow an elliptic orbit. In 1803, pebbles were dropped into a 90 m deep mine shaft in Schlebusch in Germany. Gauss and Laplace had made prediction of an expected 8.8mm deflection. The average observed deflection was 8.5mm. (Persson, 2005)
In an introductory project work for first-year university physics students, we once asked them to find out more about the motion of the earth, including ways to detect rotation. A few of the groups had found a reference to the deviation of objects dropped from a high tower. None of them had attempted to estimate the effect. After their project presentations, we interviewed all students, two or three at at time. Students from the groups that had proposed dropping objects from a high tower were all asked about the size of the effect. The answer, invariably, was "small". When asked if is would be "an Ångström or a meter", they kept insisting on their original answer, "small". Would they be able to calculate the effect? Most groups were able to describe how the effect would arise since the top of the tower moves faster than the bottom. They thought they could work it out in less than half an hour.
An examiner hearing that students, in a project spanning a
couple of weeks, did not perform a calculation they
thought would require less than half an hour obviously asks
"Why didn't you?". An important key is
that all students first asked us to provide them with a specific tower,
including its latitude and height, h. Had the problem appeared as
an examination problem, the question would be well defined and already
have been prepared to include this information, or at least introduced
notations for the relevant variables. The students would then possibly
have found the answer that the falling object would have an excess
horizontal velocity
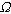h
at the
equator, which over the time of the fall would carry the object a
horizontal distance
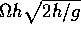
In fact, working out the deflection of a falling object in the simple way described above gives an answer that is 50% too large. During the fall, the direction of the force of gravity changes to continue to point to the center of the earth. The resulting backward acceleration can be written as
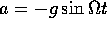
For the experiment with a marble dropping in a carousel, no complication arises due to the changing direction of gravity. The observable effect is due only to the rotation of the carousel.
Questions about how we can detect the rotation of the earth is not part of the school curriculum, not for 10-year olds, nor for 18-year olds. Even college text-books tend to omit this discussion. Section 3.2 discusses how the question of the rotating earth can be used to illutrate "Nature of Science".
In this section we analyse replies from first year engineering physics during their first week at the university, before they have had any physics classes. The engineering physics students are quite an unusual group of first-year students, as indicated e.g. by their entrance score on the often used "Force Concept Inventory" (Hestenes et al 1992, Hake, 1998) which consistently lies around 80%, before any courses at the university.
Table I presents a classification of answers given by engineering physics students. First, replies are presented from a group (I) of 110 students to the question "how do we know that the earth spins around its axis?". The second group (II) of 122 students were given an additional line "i.e. that it is not the sun moving around the earth".
| Table I: Replies to the question of "How do we know that the earth spins around its axis?". Group I received the question in this form. For group II, the line "i.e. that it is not the sun moving around the earth" was added, to encourage them to look beyond explanations referring to "day and night". | |||||||
| Group | Pendulum + Coriolis or weather | Universe + Planets | Newton | Day and Night | Seasons | Other | No Reply |
|---|---|---|---|---|---|---|---|
| I (N=110) | 4 + 3 | 12 | 5 | 26 | 2 | 6 | 58 |
| II (N=122) | 6 + 3 | 39 | 12 | 11 | 21 | 17 | 34 |
From the table we can see that less than half the students (52 of 110) answered the original question, whereas more than 70% (88 of 122) gave at least one answer to the more specific question. In both cases, only a small number of students (7 and 9, respectively) mentioned the Foucault pendulum or the Coriolis effect or weather systems.
When students were asked (at least implicitly) to look for other replies than day and night, the answers referring to the difficulty of the universe or planets moving around the earth were more common and more elaborate. In addition, a larger fraction of the students then looked to the seasons for explanation.
A small number of replies (5 and 12, respectively), were classified a referring to Newton's laws. These included replies that compared the masses and gravity of sun and earth, the difference in gravity or radius between the equator and the poles or discussed the orbits of spaceships. Two replies from group II, classified as "other" referred to the earth magnetic field.
A few students brought up more than one way to detect the rotation, e.g.
"We can see that we rotate relative to other stars and galaxies, which couldn't all move equally fast around the earth. At a certain altitude, satellites can be geostationary, without losing altitude. This indicates a rotation, where the acceleration of gravity acts as a centripetal acceleration.""By studying the sky. Also by measuring the variation of gravity over the earth. It is lowest at the equator due to the rotation."
Among the replies that were classified as "Other" in Table I were a few (3 and 4 respectively) referring non-specifically to "observations"". In group II, the "other" results also included 2 replies referring to Galileos explanations, 4 replies claming that rotation is relative, and onte reply noting that "I have never thought about it".
We conclude that the knowledge about how to detect the rotation of the earth is not widespread even among our top new physics students. Still, we have seen from interviews and discussion that even young learners can appreciate experiments designed to demonstrate the rotation of slow carousels, and be fascinated by the connection to the demonstration of the rotating earth.
Many students make reference to the motion of all the planets or stars, compare the gravity from Sun and Earth, or give other explanations within the framework of Newtonian mechanics. In these replies, the students, more or less consciously, use the criterion that many different results in science are connected, and can be explained in terms of a few fundamental particles and interaction. In this case, they refer to Newton's laws and known properties of gravity and mass.
Another aspect of scientific work is to make quantitative predictions for planning an experiment and comparison of results. In the case of objects dropping from a high tower, discussed in section 2.3, a scientific approach would include working out a formula, and pick a high tower with some "typical values" to determine if the experiment would be feasible. We find that this aspect needs to be given further attention in education.
In planning lessons for young learners, it is natural to build on strongly visual experiments and, if possible, also on the experience of the body. What can be learned by fourth-graders (10-11-year olds) from a lesson in a playground or in an amusement park? Earlier group interviews in connection with such activities have been analysed e.g. by Bagge and Pendrill (2002), Nilsson et al (2004), and Nilsson (2005).
The carousel experiments described in this paper give first-hand experience with the fictive "Coriolis force" acting on objects moving in a rotating coordinate frame. The Coriolis force is certainly not part of the school curriculum. When students encounter the mathematical treatment at university, in general, they have no direct experience of it, and find it a very abstract phenomenon, which little relevance for life nor technology. Still, experiments in slowly rotating system have been found to fascinate 10-year old learners, as well as older students. Find a playground close to you and try them out!
Ann-Marie Pendrill is professor in physics at Göteborg University, with a background in computational atomic physics. Her teaching involves engineering, physics and teacher programmes and she is involved with different forms of informal learning, including amusement park physics.