What is up? What is down? What is a straight line? With beating heart we face the unusual movements.
An amusement park is a large hands-on physics laboratory, full of rotating coordinate systems, free-falling bodies and vector additions. It gives ample opportunity to experience Newton's laws with eyes, hands and body. The amusement park Liseberg in Göteborg is the largest amusement park of Scandinavia. It has long physics traditions - Albert Einstein gave a talk at Liseberg 1923! Liseberg has many rides well suited for physics investigations, using simple equipment, as well as electronic accelerometers. Some investigations can easily be adapted to the local playground.
The heartbeat responds in different ways, both to the various accelerations and rotations of the body, but also to the thrill already in the queue. It can be monitored with electrodes on the body and the signal sent down to ground to be viewed in real time by the classmates.
A good starting point is the carousel with swings shown in Fig. 1.
As the carousel rotates, the swings hang out from the vertical line,
thereby enabling the chains to provide the force giving the required
centripetal acceleration, while still counteracting the force of gravity.
Take a
moment consider which swings will hang out the most:
the empty ones or the ones loaded with a child or with
an heavy adult! In this situation
students often pick the most heavily-loaded swings.
They watch in amazement as the carousel starts -
all swings (at the same radius)
hang at the same angle, independent of load.
This is an eye-catching example of the equivalence principle: The angle is determined by the ratio between the centripetal force and the weight. Since the intertial mass (entering the centripetal force) and the gravitational mass (entering the weight, mg), are equal, the angle is independent of the mass. Eötvös used the rotating earth as a giant merry-go-round by letting weights of different material balance from a rod suspended as a torsion balance. Refined Eötvös experiments are still performed, e.g. at the Eöt-Wash group at university of Washington, giving lower and lower limits for possible deviations from the equivalence principle./1/
Some exercises for the reader:
Many amusement park now offer visitors the possibility to experience "two seconds of weightlessness". One example is the Space Shot, ("Uppskjutet") at Liseberg. After a quick tour up, the seats are decelerated to a stop before starting the free fall. Following the fall it lands softly on an pressurized air. (The Free Fall e.g. at Gröna Lund in Stockholm, is instead decelerated by eddy currents produced by strong magnets.) The experience of weightlessness can be enhanced by taking along a small mug of water (1 cm of water is quite enough) and watch the water falling (don't pick a seat with headwind!). In the right conditions, the water seems to move slowly upward. Try it!
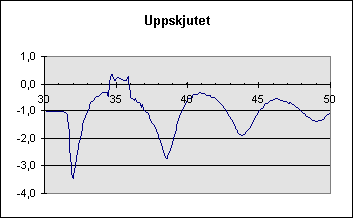Figure 2: Accelerometer data for the space shot.
The vertical axis is chosen so that standing on the
ground gives "-1g".
From the figure we see that the rider experiences about 3.5 g for a short
moment at the start and after 1.5 s of approximate weightlessness
experiences 2.5g, the 2.0g etc during the bouncing off the pressurised air.
| Often, the accelerations in an amusement park instead cause the rider to be significantly heavier than usual. "The Space Shot's emphasis is on the sudden blast upward from the bottom." /2/ Fig 2 shows accelerometer data for the space shot, obtained with a "calculator based laboratory" (CBL) connected to a graphical calculator. The data can also be used to estimate the velocity at various points of the ride, and even the position. It is a good exercise in numerical sensitivity; The resolution of the accelerometer is about 0.013g. What is the resulting uncertainty in the position after the ride (where, of course, we know that the rider is safely back to the starting point)? |
A more visual accelerometer is provided by a slinky.
Fig. 3 shows three slinkys, one unloaded, one stretched by external
forces, and one hanging free. Note how the spacing of the
turns of the hanging slinky increases with the increasing load from the lower
turns.
A few exercises for the reader:
In an amusement park, the body is exposed to a large variety of unusual
movements. How does it respond? One obvious measure is the pulse.
For attractions, like the "Space shot",
wher the largest accelerations happen within
time scales of seconds or shorter, the resolution of the heart beat is somewhat
low. The slow pendulum shown in Fig. 4 is ideal for studying the reactions of
the heart. Fig. 5. shows accelerometer data from the ride
(with the accelerometer pointing straight down to the seat
throughout the ride).
As seen from the data, the swing goes from one side to the other in about
10 seconds, until it finally makes it slowly over the top and
completes a few full turns. The baroreceptors in the body sense the
higher pressure in the head.
Standing on the ground, the observer can watch the
heartbeat dropping significantly about 2 seconds after the rider passed
the top.
One example is shown in Fig. 6. (Note: Not all rides are identical and the
accelerometer data in Fig.5 were not recorded at the same time as the
heartbeat in Fig. 6.)
Exercises for the reader:
If you visit Liseberg, you must not miss the "Lisebergbanan".
The train is
first pulled up to 65 m over sea level, giving a good
view over the city of Göteborg
and over the building site for the new Science Center "Universeum",
to be inaugurated in June 2001. The train takes
you on a 2.7 km and 2.5 minute ride, to a large extent
using the natural hills in the park,
to a lowest point of 20 m and a maximum speed of 95 km/h.
A roller coaster is a prime example of the energy principle, where
the potential energy provided as you pass the highest point is all you have
to take you round the track. How well is the energy conserved?
A visual indication is provided by the nearby "Hangover", where the train
makes a return trip on the same track. Before starting on the return journey,
the train reaches nearly is original height, before being pulled the
last few meters to the top.
A roller coaster also provides good examples of vector addition, as the train slopes and curves in different directions. In several places the tracks are built imitate the free fall parabola.
The acceleration can be measured in several different ways. A "horizontal accelerometer" is provided by a little mass on a string, e.g. a Liseberg rabbit from one of the shops. It will bounce considerably, and needs to be stopped now and then, e.g. passing over the top of a hill. Watch the angle the rabbit makes to the track! (Remember, you and the rabbit undergo the same acceleration, but the rabbit hanging from the string does not feel the "normal force" from the seat.) The slinky can again be taken along as a vertical accelerometer, or more precise data can be recorded using electronic devices.
Exercises for the reader
After the first year, more systematic instructions and information were presented on the WWW, with help enlisted from a few students in a summer project, paid by the science faculty at Göteborg university. The pages have since been revised and extended, in view of experiences gained from working with the material in subsequent courses, and, of course, as new attractions have been added to the park. These pages, available at www.science.gu.se/slagkraft/, are now used by many schools from various parts of Sweden in their preparation for excursions to Liseberg. During the year 2000, the "FRN" provided support to enable graduate students to direct visits for school classes - and giving all of us easier access to children's thoughts.
During a visit to an amusement park the equations come alive. Second derivatives are felt throughout the body. The block on the inclined plane is replaced by a train in the slope of a roller coaster and "Gedanken experiments" from the textbooks can be realised in one of the most attractive hands-on laboratories available.
